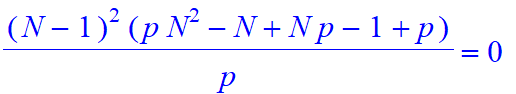
>    restart; read `c:/Users/Asus/Google Drive/Aek/Pile Game2/Pile2.txt`;

>    read `c:/Users/Asus/Google Drive/Guess.txt`;

>    #Section 4.2, Higher moments for {1,-u}, general p,q

>    #u=2, first moment, expected number

>    A:=[seq(Mo1(n,0,1,[1,-2],[p,1-p]),n=1..20)]:

>    GuessC(A,N);

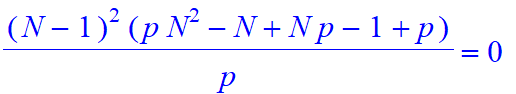
(N-1)^2*(p*N^2-N+N*p-1+p)/p = 0

>    B:=[seq(Mo1(20,s,1,[1,-2],[p,1-p]),s=0..20)]:

>    GuessC(B,S);

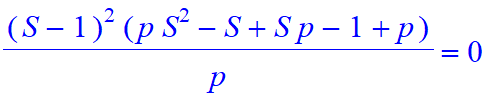
(S-1)^2*(p*S^2-S+S*p-1+p)/p = 0

>    #u=2, second moment

>    A:=[seq(Mo1(n,0,2,[1,-2],[p,1-p]),n=1..25)]:

>    GuessC(A,N);

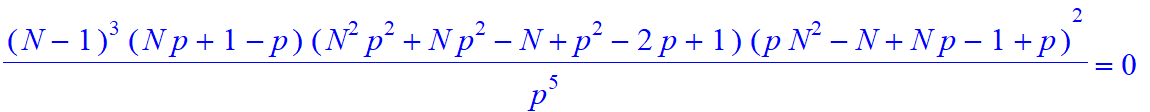
(N-1)^3*(N*p+1-p)*(N^2*p^2+N*p^2-N+p^2-2*p+1)*(p*N^2-N+N*p-1+p)^2/p^5 = 0

>    B:=[seq(Mo1(25,s,2,[1,-2],[p,1-p]),s=0..25)]:

>    GuessC(B,S);

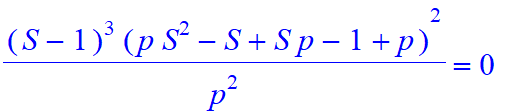
(S-1)^3*(p*S^2-S+S*p-1+p)^2/p^2 = 0

>    #u=3, first moment

>    A:=[seq(Mo1(n,0,1,[1,-3],[p,1-p]),n=1..20)]:

>    GuessC(A,N);

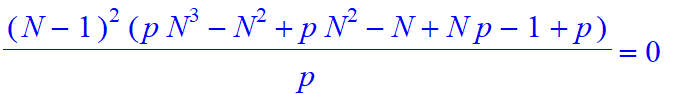
(N-1)^2*(p*N^3-N^2+p*N^2-N+N*p-1+p)/p = 0

>    B:=[seq(Mo1(20,s,1,[1,-3],[p,1-p]),s=0..20)]:

>    GuessC(B,S);

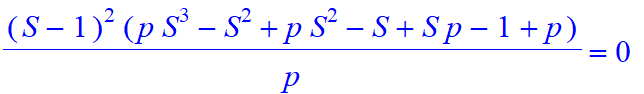
(S-1)^2*(p*S^3-S^2+p*S^2-S+S*p-1+p)/p = 0

>    #u=3, second moment

>    A:=[seq(Mo1(n,0,2,[1,-3],[p,1-p]),n=1..35)]:

>    GuessC(A,N);

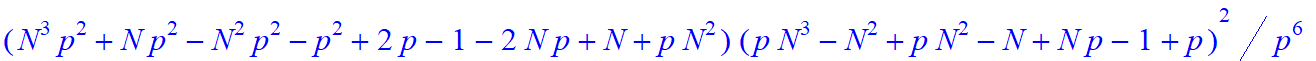
(N-1)^3*(N^3*p^2+N^2*p^2-N*p^2-p^2+2*p-1+2*N*p-N-N^2)*(N^3*p^2+N*p^2-N^2*p^2-p^2+2*p-1-2*N*p+N+p*N^2)*(p*N^3-N^2+p*N^2-N+N*p-1+p)^2/p^6 = 0
(N-1)^3*(N^3*p^2+N^2*p^2-N*p^2-p^2+2*p-1+2*N*p-N-N^2)*(N^3*p^2+N*p^2-N^2*p^2-p^2+2*p-1-2*N*p+N+p*N^2)*(p*N^3-N^2+p*N^2-N+N*p-1+p)^2/p^6 = 0
(N-1)^3*(N^3*p^2+N^2*p^2-N*p^2-p^2+2*p-1+2*N*p-N-N^2)*(N^3*p^2+N*p^2-N^2*p^2-p^2+2*p-1-2*N*p+N+p*N^2)*(p*N^3-N^2+p*N^2-N+N*p-1+p)^2/p^6 = 0

>    B:=[seq(Mo1(35,s,2,[1,-3],[p,1-p]),s=0..35)]:

>    GuessC(B,S);

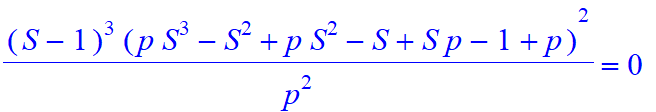
(S-1)^3*(p*S^3-S^2+p*S^2-S+S*p-1+p)^2/p^2 = 0

>